얼마 전 넷플릭스에서 중국의 유명 SF 소설 삼체를 원작으로 한 드라마를 공개했다. 원작이 워낙 뛰어난 상상력으로 구성된 작품이기도 해서 기대를 하고 시청했는데 나름 흥미로운 내용을 담고 있어 재미있는 경험을 할 수 있었다. ‘삼체(The Three Body Problem)’라는 제목은 사실 물리학, 수학, 천문학에서 중요한 문제로 꼽히는 ‘삼체문제’에서 가져온 단어이다. 드라마 속에서도 초반, 중반부까지 중요한 요소로 작용하는 이 ‘삼체문제’가 정확하게 무엇을 말하는지 알게 되면 내용을 조금 더 잘 이해할 수 있지 않을까.

삼체문제는 중력 작용으로 서로에게 영향을 주는 3개의 천체 사이 움직임을 해석하는 문제를 의미한다. 우리는 지구가 태양의 중력으로 공전을 하고 우주 공간을 움직이고 있다는 사실을 알고 있다. 그리고 그 움직임이 어떤 방식으로 진행되는지 역시 뉴턴 덕분에 알고 있다. 이처럼 태양 주변을 행성이 타원 궤도로 도는 것은 태양과 행성 사이에 작용하는 이체 문제(The Two Body Problem)이다. 삼체문제는 여기에 한 개의 천체가 추가되는 것이다.

이체 문제를 해결하기 위해서는 뉴턴의 중력 방정식만으로는 부족하다. 약간의 수학적 도구가 추가되어야 하는데 이것이 바로 미적분이다. 행성이 움직이는 순간 위치가 변하면서 주어지는 만유인력이 달라진다. 주어지는 힘이 달라지면 당연하게 가속도가 달라지고 가속도가 달라지면 속도 역시 달라진다. 속도가 달라지면 다시 위치도 변화한다. 이처럼 변화하는 것이 많기 때문에 미분방정식을 통해 그 해를 구하게 된다. 이런 방식은 뉴턴 역시 알고 있던 내용이었다. 애초에 미적분의 창시자 중 한 명이 뉴턴인데 당연한 일일 것이다.

그런데 두 가지 물체 사이에서의 관계는 미분방정식을 이용해 답을 찾아낼 수 있지만 한 가지가 추가되는 순간 내용이 달라진다. 단순하게 한 가지 천체가 추가되었는데 왜 힘든 것일까? 한 천체에 주어지는 두 천체의 중력의 합을 구하려고 해도 여기에 두 천체의 움직임이라는 변수가 다 포함되어야 한다. 복잡함의 단계가 단순히 한 단계 증가하는 수준이 아니었다. (일반적인 삼체 문제에서 답을 얻으려면 적분만 18번을 해야 한다. 그런데 얻을 수 있는 것이 10개뿐이다.) 뉴턴 역시 세 가지 천체를 통한 삼체문제에 골머리를 썩고 있었다. 이 문제는 당시 뉴턴에게 해결해야 하는 문제였다. 당장 태양과 지구, 달의 움직임이 엄밀하게 삼체문제였기 때문이다.
그나마 다행이라고 할만한 것은 태양-지구-달의 체계에서 태양의 힘이 워낙 압도적이기 때문에 태양이 주는 힘으로만 계산하여도 큰 문제가 없었다는 점이었다. 거리 상으로도 매우 가까운 지구와 달을 하나로 묶어(지구와 달의 질량 중심은 지구 안에 있다.) 태양과의 이체 문제로 바꿔도 무방했다. 다만 삼체문제가 난제라는 것은 달라지지 않았다. 수많은 수학자들이 이 난적을 물리치기 위해 뛰어들었다. 수학 역사상 손꼽히는 천재였던 레온하르트 오일러, 프랑스의 대표 수학자 중 한 명인 피에르시몽 라플라스, 역시 비슷한 시기 다양한 수학 분야에서 업적을 남긴 조세프루이 라그랑주 등 학문 역사에 발자국을 크게 찍은 거인들이 그 주인공이었다.

이들 역시 삼체문제의 일반적인 답을 얻는 것에는 실패하였다. 대신 특수한 경우에 해당하는 답은 구해내는 것에 성공했다. 라그랑주는 1772년, 같은 평면 위에 움직이는 다른 두 천체에 비해 나머지 한 천체의 질량이 매우 가벼울 경우 움직임이 예측 가능한 위치를 알아냈다. 무려 다른 두 천체에서 오는 중력이 0이 되어 정지해 있을 수 있는 위치였다. 사실 이미 오일러가 이 문제의 답을 3개나 찾아놓은 상태였고 라그랑주는 두 개를 추가하여 총 5개의 위치를 표시했다. 당시 라그랑주는 자신이 찾은 답이 너무나 특수한 경우라 생각해 특별하게 사용할 생각을 못 했지만 현재 이 위치들은 라그랑주 점이라 불리며 상당히 유용하게 쓰이고 있다. 실제로 여러 탐사선이 지구와 태양 사이의 라그랑주 점을 향해 항해했고 그 위치에 있는 경우가 많다. 적은 에너지로 궤도를 유지할 수 있으며 용도에 따라 위치를 고정할 수 있다는 것 자체가 유용했기 때문이다.
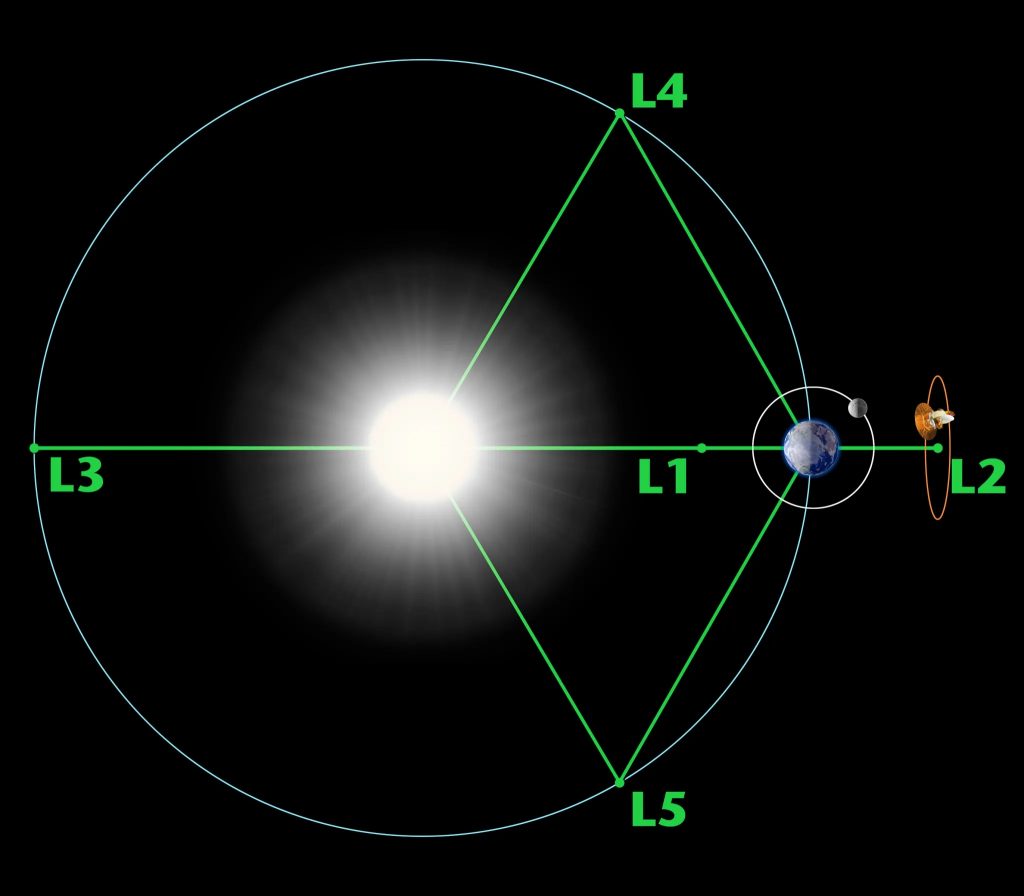

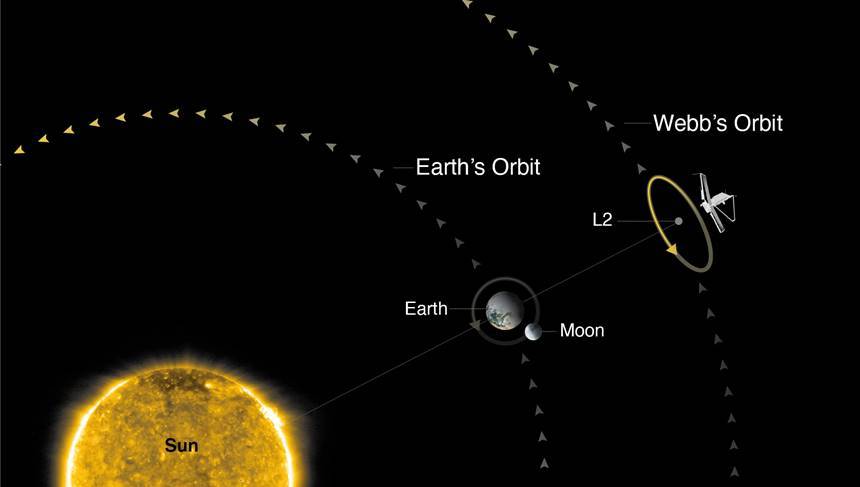
아주 특별한 몇몇 경우에 답을 찾아냈지만 여전히 일반적인 답은 오리무중이었다. 라그랑주 이후 약 100년이 지난 1887년, 스웨덴의 오스카 2세는 자신의 생일을 기념하여 특별한 이벤트를 열었다.
“뉴턴 법칙을 따르는 많은 입자계에서 충돌하지 않는 각 입자의 좌표를 시간 함수로 나타낼 것.”
이 문제는 삼체도 아니고 더 많은 물체의 움직임을 다루는 다체 문제라 할 수 있다. 이 문제에 여러 학자가 도전했지만 상을 받은 사람은 2년 뒤에야 등장했다. 프랑스의 수학자였던 앙리 푸앵카레가 그 주인공이었다. 푸앵카레는 삼체문제를 단순화시키는 방식으로 해법을 찾으려 했다. 라그랑주처럼 세 천체 중 하나의 질량을 매우 작게 만들어 이체 문제와 비슷하게 단순화시킨 것이었다. 이 과정에서 오히려 특이한 것을 증명하게 되는데 삼체문제의 일반 해를 구하는 것이 불가능하다는 내용이었다. 결국 그는 삼체문제를 ‘풀 수 없는 것’으로 확정한 것이다. 1889년 푸앵카레가 상을 받은 논문이 출판되는 과정에서 심각한 계산 오류를 발견하였고 이를 수정하기엔 이미 초판이 인쇄된 후였다. 푸앵카레는 이미 나온 초판을 폐기하고 새로 교정하는 작업을 하는데 (이 때 비용을 푸앵카레가 부담하게 되는데 상금보다 폐기에 쓴 비용이 더 컸다.) 이런 혼란스러운 과정을 거쳐 나온 논문에는 특별한 씨앗이 심어져 있었다.

그가 계산을 통해 삼체문제가 해결할 수 없음을 알던 과정 중에는 아예 그리는 것이 불가능할 정도로 복잡한 결과물이 나오는 경우도 있었다. 주어지는 천체의 초기 속도나 위치가 아주 약간만 변화해도 그 결과가 어마어마하게 달라진다는 것을 보였다는 점에서 푸앵카레의 이야기는 훗날 떠오르게 되는 ‘카오스 이론’을 나타내고 있었다. 카오스 이론은 푸앵카레 이후 1960년대 수학자이자 기상학자였던 에드워드 로렌즈에 의해 확립된 이론이다. 그가 사용한 ‘나비 효과’라는 단어가 이 이론을 잘 설명하고 있다. 나비의 작은 날갯짓이 거대한 폭풍이라는 예측하기 힘든 결과물을 가져왔다는 것으로 카오스 이론에서 초기 조건이 얼마나 중요한지 보여준다.
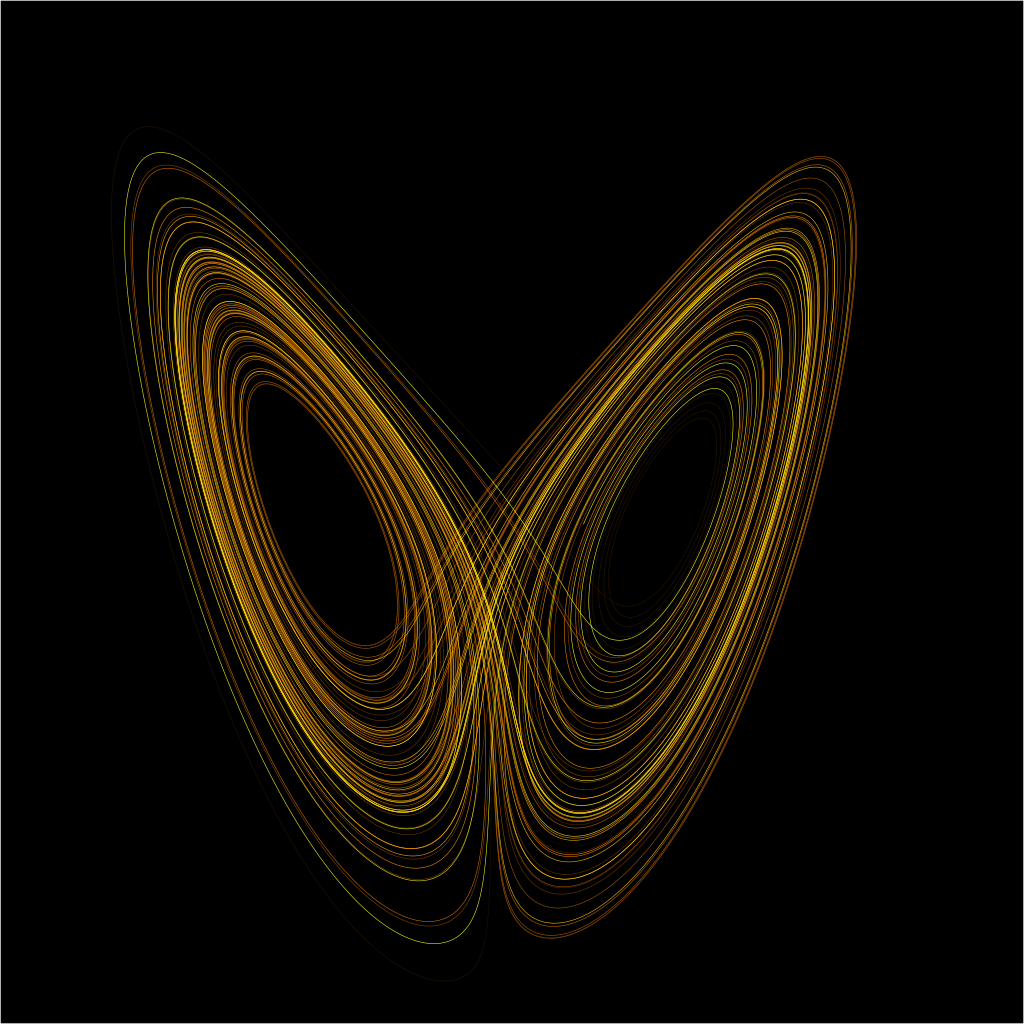
푸앵카레의 삼체문제에서 출발한 카오스 이론은 현재 굉장히 다양한 분야에서 활용되고 있다. 기체나 액체가 움직이는 난류를 예측하는 것은 기상 예측과 정확하게 결합되어 있다. 우리의 기상 예보가 100%가 될 수 없는 이유가 카오스 이론에 있다. 이 외에도 우리 몸에 있는 생체 신호에서도 카오스 현상을 찾을 수 있으며 주가, 환율 같은 경제 시장에서도 카오스 이론을 적용시켜 연구할 수 있다. 인간 세계의 복잡함을 설명하기 위해 카오스(혼돈)가 사용되는 것이다.
드라마 속에 등장하는 삼체인들은 자신들의 항성계에 무려 별이 3개나 존재한다. (이럴 경우 사실 삼체인은 3개의 별과 1개의 행성인 4체 세계에 있는 것이긴 하다.) 우리보다 훨씬 예측하기 어려운 삶을 살아갔을 그들은 혼돈에 더 익숙한 종족일 것이다. 생존하기 위해 더 빠르게 혼돈의 세상을 느껴야 했을 그들은 과연 어떤 것을 보았을까. 뉴턴의 법칙을 통해 과거, 현재, 미래의 모든 것을 예측할 수 있다는 결정론에 빠져 있던 우리가 혼돈을 제대로 마주한 것은 채 100년이 되지 않았다. 삼체 드라마를 보면서 누군가는 우주적으로 커지는 스케일에 혹할 수 있을 것이다. 하지만 내가 더 궁금한 것은 그들이 삼체문제를 통해 보았을 그 무언가이다. 과연 그들은 삼체 속 혼돈에서 어떤 것을 보았길래 그리 대단한 기술과 능력을 지녔을까. 우리는 앞으로 드라마 속 그들처럼 혼돈 속에서 본 무언가를 통해 더 거대한 다음을 찾을 수 있을지 그것이 궁금해진다.

참고자료
- 이언 스튜어트 (김지선 역). 2016. 세계를 바꾼 17가지 방정식. 사이언스북스
- 양자학파 (김지혜 역). 2021. 공식의 아름다움. 미디어숲
- 리여우화 (김지혜 역). 2020. 이토록 재미있는 수학이라니. 미디어숲
- 조던 엘렌버스 (장영재 역). 2022. 기하학 세상을 설명하다. 브론스테인
- 유용하. 2024. 얽히고설키는 3개의 중력…뉴턴도 두손 두발 든, 난제 중의 난제 ‘삼체문제’.서울신문
- 강수정. 2022. 카오스- 무질서와 질서의 틈. HORIZON
- 이재우. 2022. 삼체, 혼돈, 나비효과, 그리고 예측 불가능. NAVER Premium contents
Copyright 2021. 의왕천문소식 김용환 연구원 All right reserved.
dydgks0148@astrocamp.net